Delete the
Complexity with:
The Radius of Curvature of all Natural
Law: The
Quantity C: Possessing a Significance Far Greater than Attributed - Gravity
– As Viewed Through the Radius (VC)
- Space
as Observed through the Curve of Radius Light - Matter
and Mass - Quantum Gravity and the Holographic Mass - Beyond
A Uni-Dimensional Perception of TIME
- The
Nonlinearity of Physical Law - Integrate, make the connections: The Connected Universe
Contrast Physics’ Standard
Model perceptual confusion as shown in the contemporary synopsis articles
following. Note the issue, confusion of scale, is dominant.
The analogy of “flat earth syndrome, nose to
the ground, incapable of seeing ‘round’, is perfect characterizing today’s Standard Model (Physics)
confusion, incapable of seeing the “light”, the quantity C, the Radius of Curvature of all Natural Law........... however, the 'tiny details' are spectactular!
“….Warping, bending the
fabric of space-time may sound fancy to those still within Plato’s allegory of
the cave, however, real funding (aside from black projects) will not be
available until the ‘Snow White’ fantasy is re-construed - from complex to
simple with a common denominator….”

According to Special Relativity's time dilation and length contraction, two observers with relative motion are
condemned to eternal disagreement about times and lengths. Or are they?
They will disagree over the arbitrary times
measured in seconds and lengths measured in metres or whatever units. They
would also disagree over clock ticks, atomic vibrations and light wavelengths.
But what if there were some absolute times and lengths, determined by the very
nature of the universe? And what if these quantities could be measured in
different frames of reference. Wouldn't the observers have to agree on those
having the same value, if they agree on the same laws of physics?
Well, there is an abolute length and an absolute
time. It's possible that we'll never be able to measure them, so any threat
posed to relativity is distant and perhaps even hypothetical. It is interesting
to see whether and how these quantities might be included in relativity.
|
LP = (hG/2πc3)1/2 .
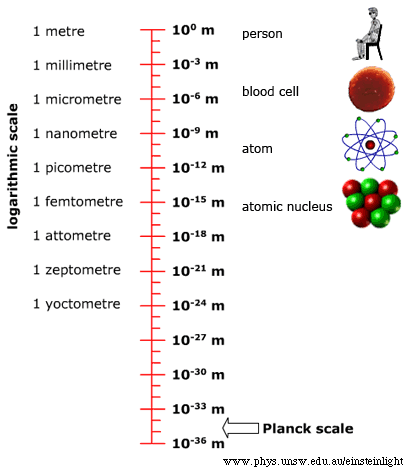
The Planck length is 1.6 x 10-35 metres.
(That's 0.000000000000000000000000000000000016 meters.) To give you an
idea, let's compare it with the size of an atom, which is already about
100,000 times smaller than anything you can see with your unaided eye (an
atom size is about 0.0000000001 meters). Suppose that you measured the
diameter of an atom in Planck lengths, and that you counted off one Planck
length per second. To measure the atomic diameter in Planck lengths would
take you 10,000,000 times the current age of the universe. (After which time,
for Joyce fans, the fires of hell may well have begun to begin to burn.)
Divide the minuscule Planck length by the speed
of light (which is pretty big) and you get a really tiny unit of time, the Planck
time, tP, which is:
tP = (hG/2πc5)1/2 .
The Planck time is 5.4 x 10-44 seconds.
(I'm wearing out the zero key on this keyboard, so I shan't write it out in
full but you get the idea: it's brief.)
There is also a Planck mass, which is (ch/2πG)1/2 =
22 μg. This doesn't sound very much, until you think of a fundamental
particle with that mass. Or until you convert it into energy by multiplying
by c2 to get 2.0 109 joules or 1.2 x 1028 eV.
Yes, 2 billion joules all concentrated in one atomic particle.
Anyhow, the Planck length and time are very
small, but they are results solely of the values that appear naturally in our
physical laws. So according to the principle of Special Relativity, it seems
that different observers should observe them to be the same. So what about
time dilation and length contraction? If these lengths and times are
observable as physical lengths and intervals in moving frames, it appears
that we shall need to modify Special Relativity to include them. One theory
that does so is called Doubly Special Relativity, suggested in 2002 by
Giovanni Amelino-Camelia.
Before we get too excited, we should point out
just how far beyond current experimental technology these effects are.
Particle accelerators are described by the energies that they can produce,
and the latest generation produces energies of TeV, or 1012 eV.
The Planck energy is 1.2 x 1031 eV. We are short by
a factor of 1019. Which is a good thing.
Further, it's not clear (to this author, at
least) what it would mean to measure these lengths and times in or from
different frames of reference. As we'll see below, on the Planck scale, time
and space no longer have their ordinary, macroscopic meaning and so naïve
applications of relativity are probably inappropriate.
|
Quantum mechanics, gravity and relativity
So, where do these quantities come from? The
speed of light c is the natural unit that relates time and space. G is the
constant of gravity, and h is the constant of quantum mechanics. So the Planck
scale defines the meeting point of gravity, quantum mechanics, time and space.
Currently, we don't know much about this interaction, because gravity is so
feeble that its influence on things as small as quantum systems is small.
Special Relativity and quantum mechanics work
very well together. Relativistic quantum electrodynamic is a spectacularly
accurate theory. Richard Feynman once described how accurate it was by saying:
if you asked me how far it was to the moon and I said "do you mean from my
head or from my feet?" That accurate.
Quantum mechanics and gravity (whether Newton's
theory of gravity or Einstein's theory of General Relativity) do not fit so
neatly together. The problem can be put in several different ways, but I favour
this one. From our discussion of virtual particles (Why
there would be no chemistry without relativity), we saw that virtual
particles could be larger (ie more massive) if their lifetime and range were
smaller.
Now both Newton's and Einstein's gravity predict
that enough mass in a small enough space can produce a black hole: a region
with a gravitational field so strong that its escape velocity is c. When we put
the two ideas together, we find that there is a scale small enough for virtual
black holes to exist. This is the Planck scale. On this scale, all of the
weird, singular behaviour associated with black holes asserts itself. Space and
time as continuous entities cease to have meanings when discussing distances of
10-35 metres and times of 10-44 seconds. So
relativity, a theory of space and time based on a continuum, must run into
serious difficulties.
Which is perhaps not surprising: the Planck scale
is a very, very long extrapolation from our current knowledge.
On this topic, we have so little direct knowledge
that there are few hints to guide the development of theories, and even fewer
constraints upon those theories. Consequently, there are several different
families of theories that aim to produce a consistent theory of quantum
gravity. Usually they include a larger number of spatial dimensions, not all of
which are macroscopic*. At the moment, however interesting they be, these
theories are speculative. Perhaps one of them will turn out to be a good,
useful theory, and the others will fall. At the moment, we cannot put them to
the test.
Today, we remember Democritus for speculating on
the existence of atoms and Aristachos for proposing that the Earth went around
the sun. The ancient Greek philosophers proposed so many ideas that it is
perhaps not too surprising that some of them turned out to be consistent with
facts discovered much later.


No comments:
Post a Comment